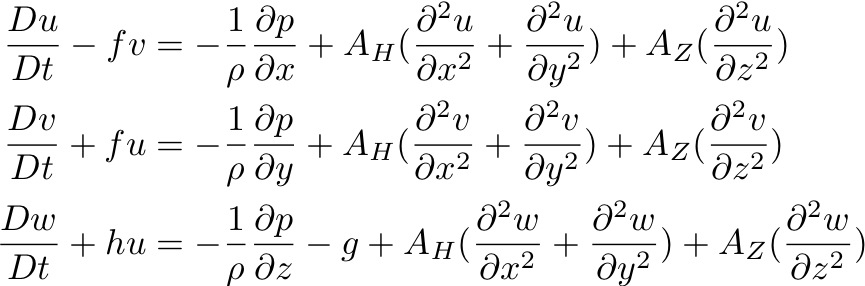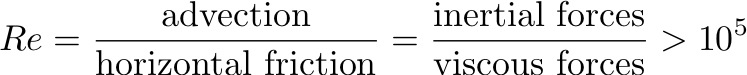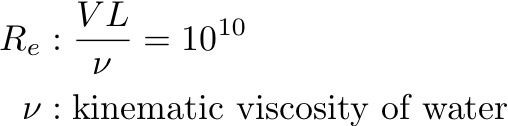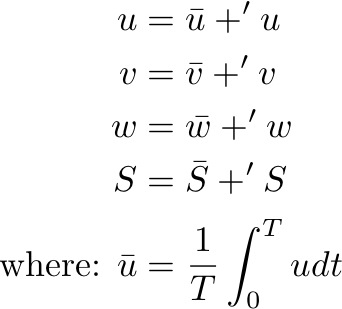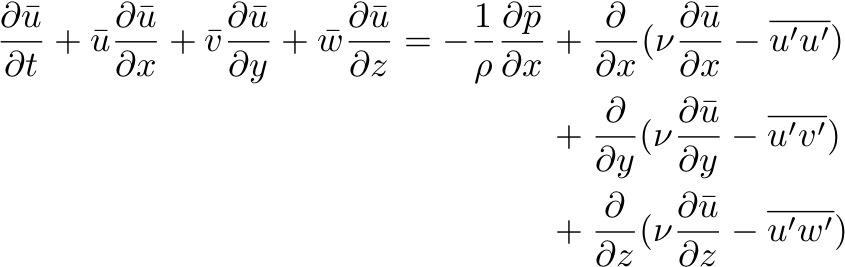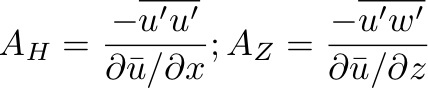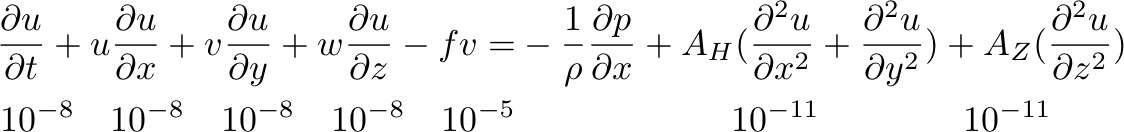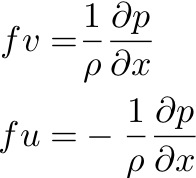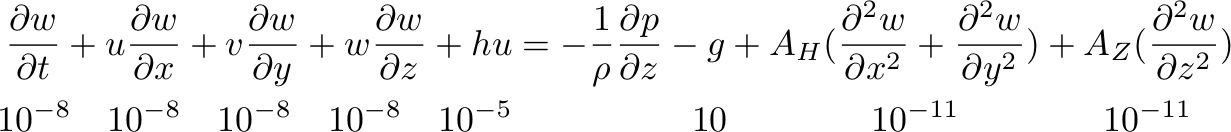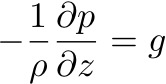Notes:
Since we cannot solve the full set of Navier-Stokes equations. The concept of scaling is thus very important. If we can quickly ascertain the most significant elements, or balances, for given flows, then we can simplify the equation set with appropriate approximation, and obtain proper solutions.
The Navier-Stokes equations:
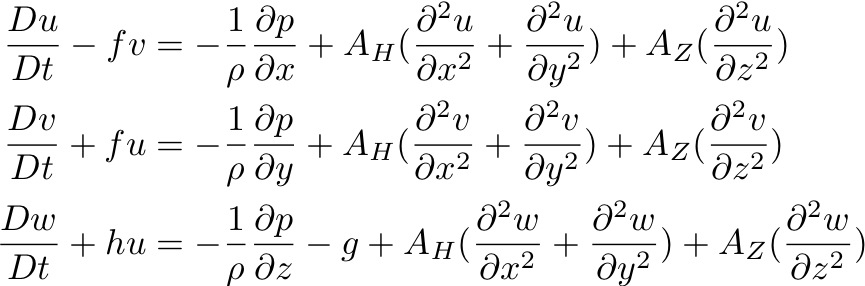
In order to scale the equation, it is useful to understand the sizes of the eddy viscosities/diffusions, AH, AZ, sometimes called Reynolds stress or turbulent stress, because Reynolds was the first to put forward the analogy between molecular viscosity turbulence viscosity. Neither AH nor AZ can be directly calculated, but instead can be empirically estimated through experiments and measurements.
Turbulence in the ocean leads to mixing. Water parcels are displaced by turbulence, which leads to a transfer of momentum or other properties (S, O2...) from one place to another.
In the vertical, the displacement of water parcels has to work against the stability of the water column, against the buoyancy forces. Vertical requires more energy than horizontal mixing, and therefore isopycnal mixing is much larger than diapycnal mixing, namely AH >> AZ.
However, vertical mixing is important because it changes the stratification of the water column and controls, to a large extent, the rate at which deep water eventually reaches the surface ocean (ventilation).
How do we know that the ocean is turbulent? Reynold ran many laboratory experiments, and found that if the Reynold’s Number Re of two flows are equivalent, they will behave the same, no matter the scale of the flow. He further found out that for Re > 105, a flow is always turbulent.
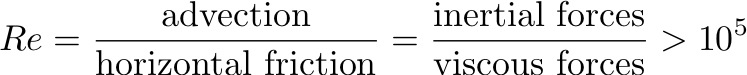
For typical ocean scales:
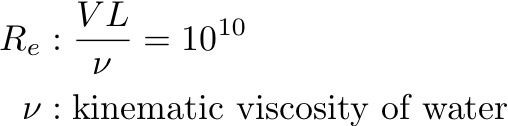
How do we present this turbulence in a flow fields? We need to decompose the flow field into the slow laminar processes that we can describe and the fast turbulence processes that we need to parametrize. So how do we separate the steady displacements from a fluctuating ones? We break down the flow fields into mean and fluctuating components:
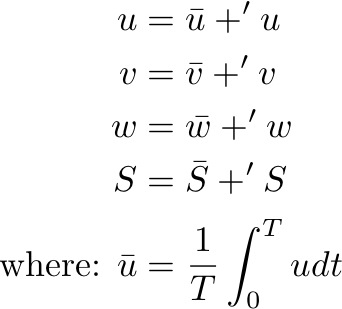
Reynolds expanded the momentum equations using the above decomposition and integrated over a timescale T to find the Reynolds' stresses in terms of the fluctuating fields.
So defining eddy viscosity in the same way as molecular viscosity, Reynolds found that:
Horizontal mixing: AH has dimensions of UL, and thus changes with different scales of flows. Measurements suggest that:
- AH ~ 8 x 102 m2s-1: Geostrophic horizontal eddy diffusivity;
- AH ~ 1 to 3 m2s-1: Open water (breaking of internal waves).
Vertical mixing: Walter Munk (1966) made a very important estimate of average viscosity by observing that the thermoclinedoes not change over decades. A steady-state thermocline requires the downward mixing of heat by turbulence must be balanced by an upward transport of heat by a mean vertical current, such that:

Munk estimated the average vertical velocity using observations of radioactive isotopes 14C, obtaining an vertical eddy viscosity AZ= 1.3 x 10−4 m2s-1. Globally, Munk’s theory requires 25-30 Sv of deep water formation.
NS equations scaling:
We use following typical values:
- Horizontal speed, V = 0.1 ms-1
- Time, T = L/V = 107 s
- Horizontal length, L = 106 m
- Coriolis, C = 10-4 s-1
- Gravity, g = 10 ms-2
- Vertical speed, w = 10-4 ms-1
- Vertical length, H = 103 m
Consider the horizontal momentum equation:
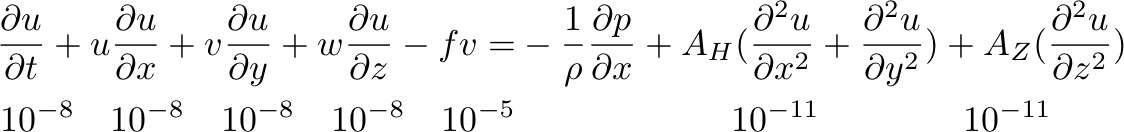
So, the balance of terms for large scale ocean circulation is geostrophic:
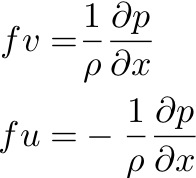
Now consider the vertical momentum equation:
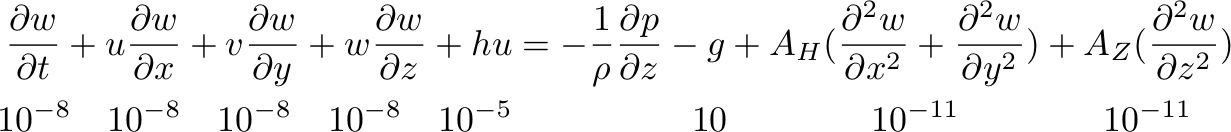
We obtain the hydrostatic balance:
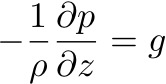
There are a number of dimensionless numbers which are useful for ascertaining the relative importance of the different components of the flow, in general. These are used extensively in GFD to simplify the NS equations.
If Ro is small, rotation is more important than nonlinear advective terms, which is true for the open ocean. Near frictional boundaries, the Ekman number becomes large and friction is more important than rotation. So the geostrophic balance will no longer holds.
Last modified: Sep 2014