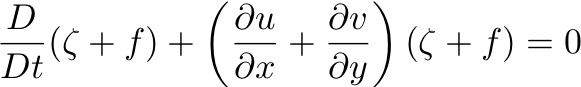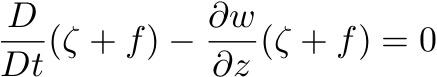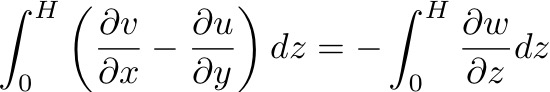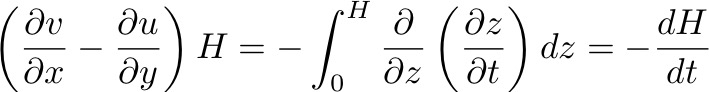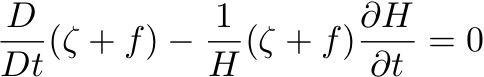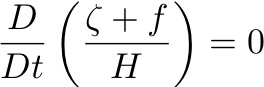Notes:
Vorticity is an important conceptual tool for understanding the nature of ocean circulation, because on a rotating Earth all scales of motion circulate: from inertial scales (1 km) to eddies at mesoscale (100 km), to ocean gyres at the large scale (10,000 km). On all these scales ,the flow has VORTICITY.
As a result, formulating the equations of motion in terms of the conservation of vorticity (similarly to the way we considered conservation of mass, heat and salt) can give some fundamental concepts of the universal qualities of rotating flows.
Mathematically, we define vorticity:
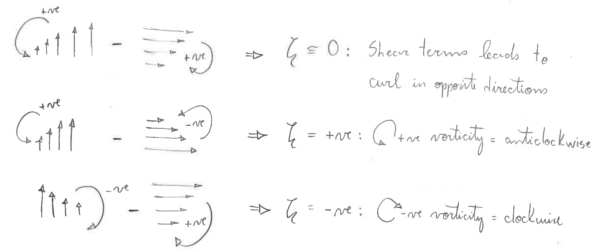
It is the spin about the vertical axis, z. More specifically, it is the shear of the meridional velocity in the zonal direction minus the shear of the zonal velocity in the meridional direction. IF THE FLUID FLOW HAS SHEAR, IT HAS VORTICITY.
How does this work?
This vorticity, ζ, that results from the shear of the local fluid flow is called RELATIVE vorticity. It is the spin of the fluid relative to the Earth.
Everything on Earth also has a PLANETARY vorticity, f, which we have seen is twice the local rotation rate of the planet.
Notice that if f is greatest at the poles, is zero at the Equator and is negative in the Southern hemisphere, where latitude is negative by definition.
The sum of the RELATIVE and PLANETARY vorticity is called ABSOLUTE vorticity, ζ + f.
So, lets look at the momentum equations in terms of vorticity and see what we can learn about the flow.
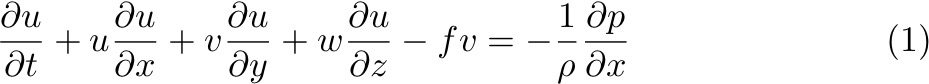
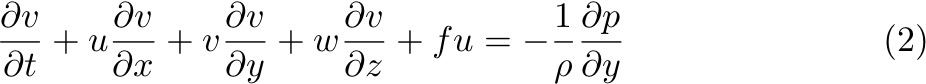
Assume frictional terms are small (away from Ekman layers), and density terms are small. Cross-differentiate these equations as:
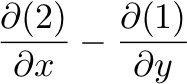
Which leads to:
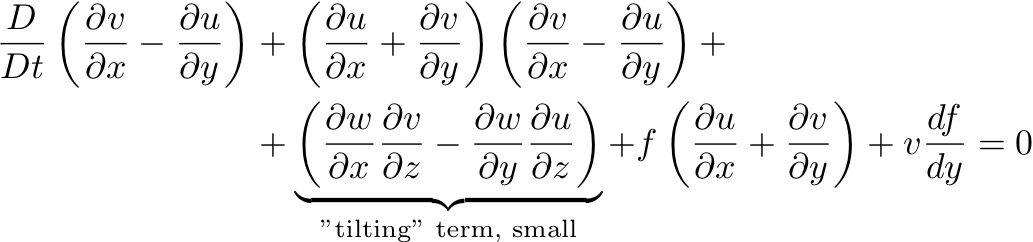
Substitute for 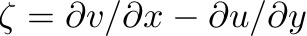 :
:
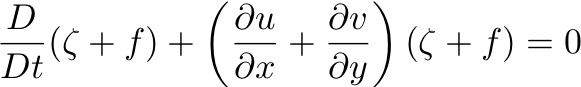
Which is the VORTICITY EQUATION. By using continuity, the divergence term above can be also be written as:
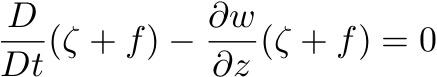
It is useful to consider this vortex stretching term in terms of a layer thickness, H - that is, in terms of a vertical velocity w pumping water into or out of the layer and hence local thinning or thickening. This "stretching" of the layer is going to cause a change to its spin or vorticity.
So, considering layer thickness H, within which ρ is a constant and thus velocities u and v are constant, integrate the continuity equation over this thickness:
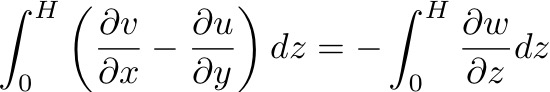
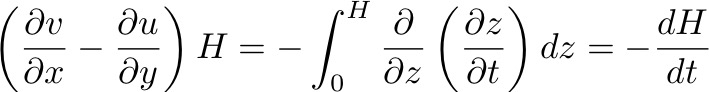
Substituting for the horizontal divergence in the vorticity equation we get:
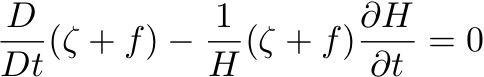
Which can be written:
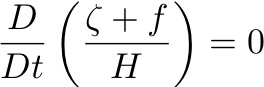
So, in the interior of the ocean, where friction can be considered negligible and hence there is no transfer of momentum between fluid parcels, POTENTIAL VORTICITY is CONSERVED.
The conservation of PV couples changes in relative vorticity to changes in depth, H and latitude. All three interact and balance each other.
1. Consider depth is constant and we change a water parcel's latitude:
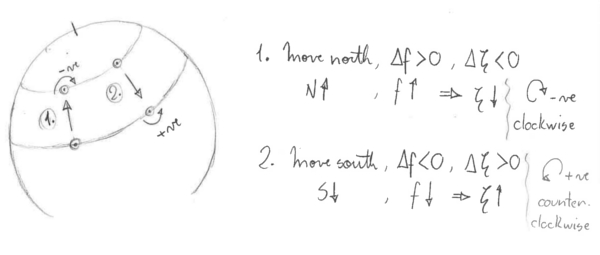
So, as a column of water moves equatorward, | f | decreases and ζ must increase. Or, consider a barrel of water initially at the north pole that is moved quickly southward where f is smaller - the water will appear to rotate counterclockwise, since it acquired positive ζ.
2. Now consider changes in depth at a constant latitude:
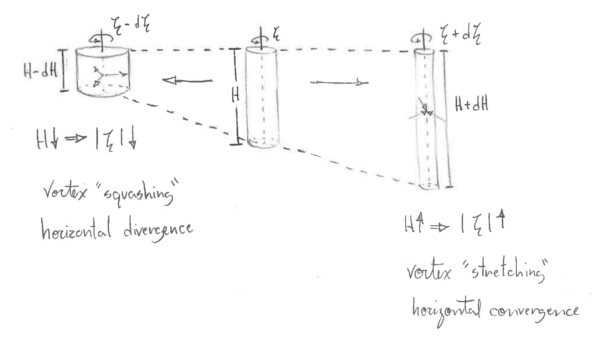
This concept is analogous with the way that ice skaters change their spin - by extending their arms outwards they increase their moment of inertial, which decreases their rate of spin, and angular momentum is conserved.
The concept of vorticity and its application to ocean circulation leads to a deeper understanding of the nature of the flows on a rotating Earth. These are a couple of examples:
- Flows tend to be zonal: In the open ocean, f << ζ and hence f/H = constant. This requires that flows in an ocean of constant depth be zonal (in the absence of an input of vorticity). Specially true close to the Equator, where ∂f/∂y is large.
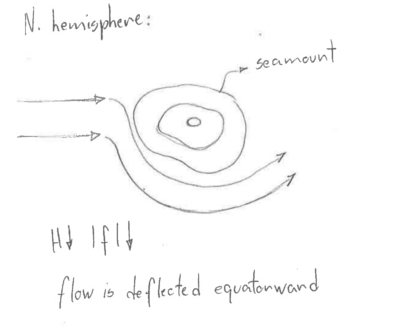
- Topographic steering: Imagine a seamount or topographic ridge in the deep ocean. Again, f/H is constant - so if Hdecreases then f must decrease and the flow is turned towards the Equator. If the change in depth is sufficiently large that a reasonable change in latitude cannot compensate, then the flow may be unable to cross the ridge. This is called TOPOGRAPHIC BLOCKING.
Last modified: Dec 2014



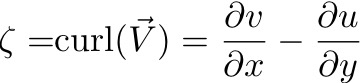

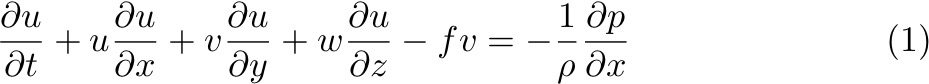
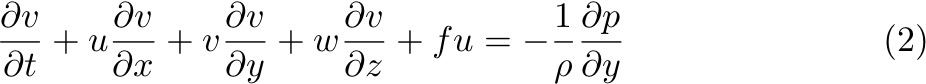
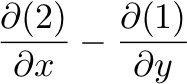
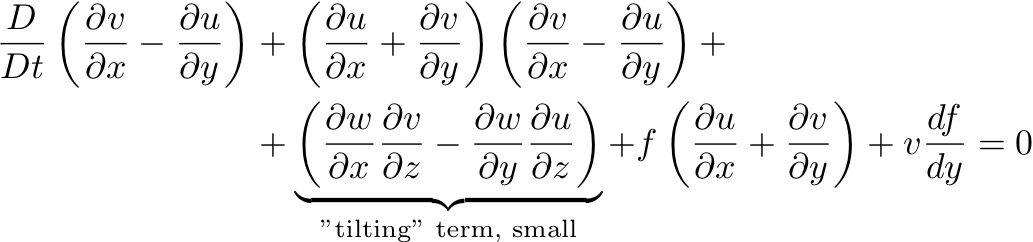
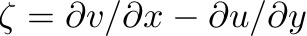 :
: